T-tests are Linear Regression

A new way to decide if your ideas are correct

Part 1: T-tests

A word problem

Adam emails Amber:

I want to know if advertising our newest trail will increase its weekend usage.

• For the next two months, count the number of people that use the trail each Saturday.
• Then, create an advertising campaign promoting the trail for two weeks.
• Finally, spend another two months counting usage each Saturday.

If there are more people that use the trail on average after the campaign, we'll keep promoting it!

Results

Amber does the study and finds that, on average:

• For the first 8 weeks, an average of 48 people use the trail each weekend.
• After the advertising, an average of 64 people use the trail each weekend.

Should Adam continue funding the advertising?

What do we want to know?

Another way of asking this question is:

Do we have enough evidence to be confident that the advertising had a positive effect on trail usage?

Naively, we could say:

64 feels way higher than 48. It's a 35% increase. The advertising seems like it's working.

It'd be nice if we could use a mathematical framework for taking the feeling out of this statement.

Digging a little deeper

Before we do any stats, let's take a deeper look at the numbers Amber collected:

df1

	0	1	2	3	4	5	6	7
week
no_advertising	58	48	47	36	49	48	47	51
advertising	42	34	35	37	43	42	33	250

What's the obvious issue here?

Lesson 1

Averages alone are insufficient to conclude whether our advertising had an effect on trail use.

What if we remove the outlier?

sns.barplot(x="week", y="count", hue="advertising", data=df1_1)
plt.show()

sns.barplot(x="week", y="count", hue="advertising", data=df1_1)
plt.show()

What just happened?!

If we remove the outlier, it looks like the advertising may actually decreases the average trail usage. But we still haven't learned what math we need to convince ourselves that advertising had some effect.

Besides the average, the other value we need to calculate about our data is the variance, or how spread out our numbers are.

Variance

• x_i = The value of one sample
• m = The average of all samples in the group
• n = How many samples are in the group
• V = Variance

$$ V = \frac{\sum{(x_i - m)}^2}{n-1} $$

Example

Let's say we have a group, [5, 10, 15]:

$$ V = \frac{(5 - 10)^2 + (10 - 10)^2 + (15 - 10)^2}{3-1} = 25 $$

More data near the average gives us a lower variance:

G2 = [5, 10, 11, 12, 15]
V2 = ((5-10.6)**2 + (10-10.6)**2 + (11-10.6)**2 + (12-10.6)**2 + (15-10.6)**2)/(5-1)
print(f"The variance of {G2} is {V2}\n\n")

The variance of [5, 10, 11, 12, 15] is 13.3

variance()

Lesson 2

• The average gives us information about the peaks of these groups.
• The variance gives us information about the widths of these groups.

Student's t-test

A t-test allows you to compare two groups using their means and their variances to decide whether or not the averages of the two groups are the same.

$$ t = \frac{m_A - m_B}{\sqrt{ \frac{\frac{\sum{(x-m_A)^2}+\sum{(x-m_B)^2}}{n_A+n_B-2}}{n_A} + \frac{\frac{\sum{(x-m_A)^2}+\sum{(x-m_B)^2}}{n_A+n_B-2}}{n_B} }} $$

In school, you're handed this formula and told to use it, with no real explanation of why it works.

p-value

There's one more concept to learn about before we can decide if the average trail usage is different after advertising. It's a number called the p-value.

• It's a decimal number between 0 and 1.
• For our usage, the smaller the p-value, the more likely it is that the averages of the two groups are different, and thus more likely that the advertising had an effect.
• By convention, if the p-value is smaller than 0.05, we say that the two groups have different averages.

Running a t-test will give you a p-value.

t-test usage

Let's tie all of these concepts together using Amber's data.

df1

	0	1	2	3	4	5	6	7
week
no_advertising	58	48	47	36	49	48	47	51
advertising	42	34	35	37	43	42	33	250

round(ttest_ind(advertising, no_advertising, equal_var=False).pvalue, 4)

0.5548

This p-value tells us that, even though

64 feels way higher than 48. It's a 35% increase. The advertising seems like it's working.

There's no mathematical evidence that this "feeling" is correct.

Without the outlier weekend

What if we remove the outlier of the last Saturday?

round(ttest_ind(advertising[:-1], no_advertising, equal_var=False).pvalue, 4)

0.0026

This p-value tells us that we have enough data to hypothesize that advertising may lower the average trail usage.

But why?

It's important to note that the t-test isn't going to provide any information on why two groups are different from each other. These results are still open for interpretation. In our case, we could imagine that:

1. The final weekend of measurement was July 4th. The trail usage was going to be really high regardless of advertising.
2. In reality, advertising had a negative effect on trail use. People who saw the advertisement actively avoided the trail because they assumed it was going to be crowded.

Lesson 3

When you hypothesize that the averages of two groups of numbers are different or not, the t-test may be able to give you a mathematical way to decide.

Part 2: Linear regression

A word problem

Emily wants to do some financial modeling. She's been a realtor for a year now, and has been tracking her savings account each week. She asks herself:

Based on my savings, when will I have enough saved to buy the unicorn I've been wanting?

Emily's spending habits are a bit unpredictable, but she really wants a unicorn, even if they're expensive. In fact, they're $1,000,000!

Results

• At the start of the year, Emily had \$12345
• At the end of the year, Emily had \$56959
• She saved \$44614
• That's \$858/week
• At this average rate, it's going to be more than 21 years before Emily can buy her unicorn.

But... what do we know about averages?

Digging a little deeper

Before we do any stats, let's take a deeper look at the numbers Emily collected.

sns.lmplot(x="week", y="savings", data=df2, fit_reg=False); plt.show()

Variance matters!

It turns out that Emily makes, and spends, a lot of money. The last handful of weeks, however, haven't been great. Therefore, just looking at Emily's current statement isn't a good estimate for when she'll likely have \$1M.

If you eye-balled a "trend line", when do you think the trendline would hit the \$1M mark?

Linear regression

"Linear regression" is a fancy way of saying "trend line", or as a third name, "line of best fit".

There's a mathematical way of determining what that line should be. Let's look at the results first.

sns.lmplot(x="week", y="savings", data=df2, ci=None); plt.show()

To place the line we minimize the distance of the points to the line, squared.

Ordinary Least Squares

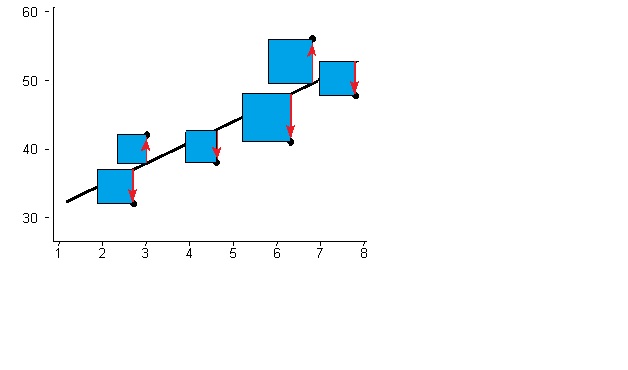
Visually, we want the sum of the area of these boxes to be as small as possible.

Stated more qualitatively: we're finding the line that minimizes how spread out our data is from the line.

Slope

The slope (or "steepness") of that line is calulated as:

$$ S = \frac{\sum_{i=1}^{n}{(x_i - \bar{x})(y_i - \bar{y})}}{\sum_{i=1}^{n}{(x_i - \bar{x})}^2} $$

For our purposes, S will represent the number of dollars Emily saves each week, on average.

If we apply this formula on Emily's data, we learn that:

1. She's saving an average of \$2321/week
2. It'll take her fewer than 8 years to buy her unicorn, instead of more than 21.

And that doesn't count of she changes her spending habits!

y-intercept

To define the line of best fit, you also need to define the "y-intercept", or the value of y when x=0. Here's the formula in our case:

$$ b = \bar{y} - S\bar{x} $$

Note: This value doesn't have a particularly meaningful interpretation for our specific word problem, though, it can be useful in other cases.

p-value

p-values are also applicable to lines of best fit. You can phrase what information a p-value tells you a few different ways:

1. The lower the p-value the better your line-of-best-fit is at describing the data
2. The lower the p-value the more predictive power you have

For Emily's data, we can calculate a p-value by:

linregress(df2["week"], df2["savings"]).pvalue

1.2967281822155235e-07

Lesson 4:

Linear regression allows you to create a line-of-best-fit for two sets of measurements you believe to be linearly correlated, and also gives you information about the strength of their relationship.

Part 3: Twist

A word problem

Erin has invented a new air conditioning device that uses ultra-low power. It cools an Arizona house for a few dollars a month. She has two different designs for the device, and must decide which to commercialize. She runs both designs for a month, measuring their power consumption every hour. Which of the two methods we've learned, a t-test or linear regression, should she use to make her decision?

Digging a little deeper

devices()

It is, of course, a trick question

While the problem is worded most similarly to Amber's trail usage problem, we can quickly show that the p-value we get from a linear regression is exactly the same, if we encode our data properly.

Dummy encoding

All we have to do is use linear regression where all of the samples from design (a) are assigned a value of 0 for their x variable, and all of the samples from design (b) are assigned 1. This is called "dummy encoding".

sns.lmplot(x="design", y="power", data=df2, ci=None, aspect=1.5, x_jitter=.05); plt.show()

Tada!

Results

print(ttest_ind(a, b).pvalue)
print(linregress(dummy, ab).pvalue)

1.94473286222529e-27
1.9447328622258202e-27

We don't have time to get into it today, but the t-test is one of the half dozen different tests that you're told to memorize in an Intro Stats class. Each of those tests can be tied back to special cases of linear regression, as explained in this excellent post.

Lesson 5

The seemingly disparate statistical concepts of t-tests and linear regression are equivalent!

Summary

• Averages alone are insufficient to conclude whether our advertising had an effect on trail use.

• The average gives us information about the peaks of these groups.
• The variance gives us information about the widths of these groups.

• When you hypothesize that the averages of two groups of numbers are different or not, the t-test may be able to give you a mathematical way to decide.

• Linear regression allows you to create a line-of-best-fit for two sets of measurements you believe to be linearly correlated, and also gives you information about the strength of their relationship.

• The seemingly disparate statistical concepts of t-tests and linear regression are equivalent!